对于前一篇文章中有说到三种基础排序算法,分别是冒泡、插入和选择排序,它们的时间复杂度都是O(n^2),比较高,适合小规模的数据排序。这一篇文章我们来讲两种时间复杂度为O(nlogn)的排序算法,归并排序和快速排序。
思考:归并排序和快速排序都用到了分治的思想,我们可以借助这个思想来解决非配许的问题,比如,如何在O(n)的时间复杂度内查找一个无序数组中的第k大元素?
归并排序(Merge Sort)
排序一个数组,先把数组从中间分成前后两个部分,然后分别对这两个部分进行排序,再将排好序的两部分合并在一起。
这里用到了 分治思想,将一个大问题分解成小的问题来解决。我们都知道递归也是将大问题分解成小问题来解决,实际上分治算法一般也都是用递归来实现的。但是前者是一种解决问题的处理思想,而递归是一种编程技巧。
下面我们来具体讨论一下归并排序:
原理:先把数组从中间分成前后两个部分,然后对前后两个部分分别进行排序,再将排序好的两个部分合并到一起。
如图: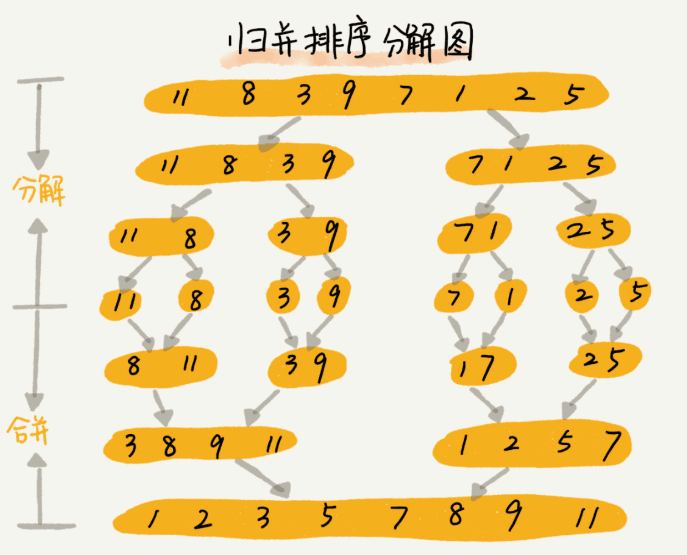
我们前面讲到,分治算法一般都是由递归来实现的,那么我们应该如何用递归来实现归并算法呢?前面我们讲过,递归最重要的是要找到递推公式和终止条件。
1 | // 递推公式: |
算法实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37// 归并排序
void merge_sort(int[] a, int left, int right) {
//终止条件
if(left >= right) {
return ;
}
int middle = (left + right) / 2;
merge_sort(a, left, middle);
merge_sort(a, middle + 1, right);
merge(a, left, middle, right);
}
// 合并两个有序的数组
void merge(int[] a,int left,int middle,int right) {
int i = left, j = middle + 1, k = 0;
int *temp = (int*)malloc((right - left + 1)*sizeof(int));
while(i <= middle && j <= right) {
if(a[i] <= a[j]) {
temp[k++] = a[i++];
} else {
temp[k++] = a[j++];
}
}
// 判断哪个子数组中有剩余的数据
if (i > middle) {
while(j <= right) {
temp[k++] = a[j++];
}
}
else {
while(i <= middle) {
temp[k++] = a[i++];
}
}
return ;
}
算法分析:
稳定性:我们通过代码可以观察到,merge_sort()是不会改变元素的顺序的,稳定性怎么样还是要看merge()函数。再观察,在merge()函数中是先将a[left..middle]中的数放入临时数组temp中,所以它不会改变相同元素原先的顺序,因此它是一个稳定的排序算法。
空间复杂度:O(n)
时间复杂度:
- 最好情况:O(nlogn)
- 最坏情况:O(nlogn)
- 平均时间复杂度:O(nlogn)
先来看时间复杂度。这里涉及递归的时间复杂度计算。在计算递归时间复杂度时,我们可以 将求解的问题写出递推公式,将代码的时间复杂度也用递推公式表示出来,从而求解出时间复杂度。当然,除了这种方法外,在树的那一节中会介绍到另一种求解方法 递归树。下面我们就用递推的方式来求一下时间复杂度。
我们假设对n个元素进行归并排序需要的时间是T(n),那分解成子数组排序的时间就是T(n/2)。我们知道merge()函数合并数组的时间复杂度是O(n)。于是就有:1
2T(1) = C; // n = 1时, 只需要常量级的执行时间
T(n) = 2*T(n/2) + n; // n > 1
现在我们知道关于T(n)的表达式了,那么我们应该如何根据已知的式子求出T(n)呢?我们来再将它们分解一下:
1 | T(n) = 2*T(n/2) + n |
这样,最后当$n/(2^k) = 1$时,可知$k = \log_2 n$(以2为底, n的对数)。将k带入就可以得到:T(n) = nlog2(n) + Cn。用O表示法时间复杂度就是O(nlogn)。
好啦,时间复杂度搞定了,那么空间复杂度怎么算呢?其实很简单,从概念出发。在任意时刻,CPU只会有一个函数在执行,也就只会有一个临时的内存空间在使用。所以空间复杂度时O(n)啦。正因为这一点,它就 不是原地排序,。
快速排序(Quick Sort)
快速排序是,如果要排序数组中下标从left到right之间的一组数据,我们选择left到right之间的任意点作为分区点pivot。遍历left到right之间的数据,将小于pivot的放在左边,大于pivot的放在右边,pivot在中间。这样:
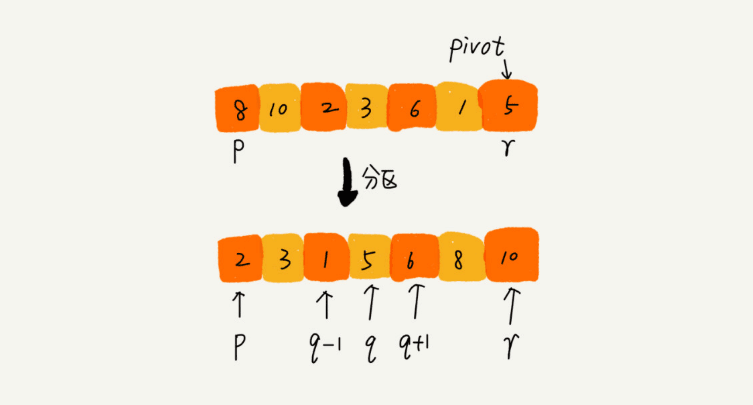
再根据分治、递归的思想,我们可以用递归排序下标从left到middle - 1之间的数据和下标 middle + 1到right之间的数据,直到区间缩短为1。所以递推公式和终止条件是这样的:
1 | // 递推公式: |
算法实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24// 快排
void quick_sort(int[] a, int left, int right) {
if(left >= right) {
return ;
}
int middle = partition(a, left, right); // 函数返回pivot的下标
quick_sort(a, left, middle - 1);
quick_sort(a, middle + 1, right);
}
// 原地分区
int partition(int[] a, int left, int right) {
int pivot = a[right];
int i = left;
for(int j = left; j < right - 1; ++j) {
if(a[j] < pivot) {
swap(a[i], a[j]);
++i;
}
}
swap(a[i], a[right]);
return i;
}
算法分析:
稳定性:因为在分区的过程中会涉及交换操作,如果数组中有两个相同的数据,经过分区操作后也会交换位置,所以 快速排序是一个不稳定的排序算法。
空间复杂度:O(1)。
时间复杂度:
- 最好O(nlogn)
- 最差O(n^2)
- 平均O(nlogn)
看起来归并排序和快速排序真的很相似,都是用的分治思想,那么它们的区别在哪里呢?
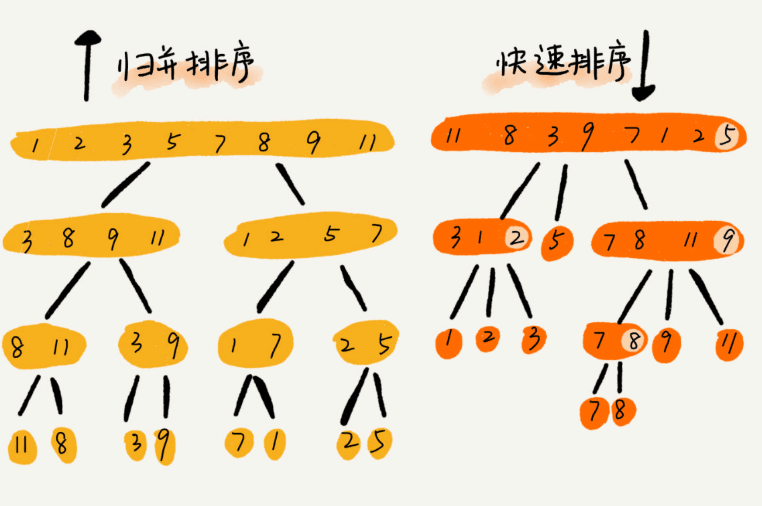
可以发现,归并排序的处理过程是由下到上而快排则是由上到下。归并排序是稳定但非原地排序算法,而快排因巧妙设计使其可以在原地分区函数实现原地排序解决了归并排序占用太多内存的问题。虽然快速排序最差情况的时间复杂度为O(n^2),但是大部分情况下的时间复杂度可以做到O(nlogn),只有在极端情况下才会退化到O(n^2)。
解答开篇
快排的核心思想是 分治和 分区,我们可以利用分区的思想来解答开篇的问题:O(n)时间复杂度内求无序数组中的第K大元素。
我们选择数组区间 A[0…n-1] 的最后一个元素 A[n-1] 作为 pivot,对数组 A[0…n-1] 原地分区,这样数组就分成了三部分,A[0…p-1]、A[p]、A[p+1…n-1]。如果 p+1=K,那 A[p] 就是要求解的元素;如果 K>p+1, 说明第 K 大元素出现在A[p+1…n-1] 区间,我们再按照上面的思路递归地在 A[p+1…n-1] 这个区间内查找。同理,如果 K < p+1,那我们就在A[0…p-1]区间查找。
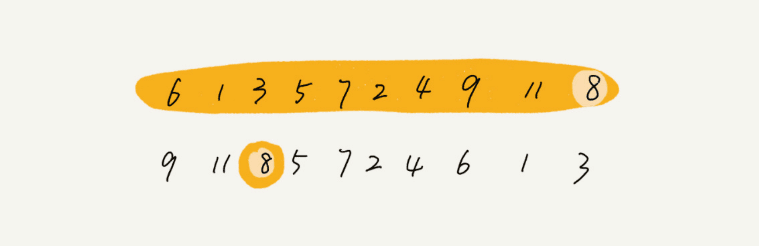
我们再来看看它的时间复杂度为什么是O(n)呢?第一次分区查找,我们需要对n个数进行分区操作,第二次是n/2,以此类推,我们可以很容易的看出它是一个等比数列,因此总的复杂度是:n + n/2 + n/4 + … + 1 = 2n - 1。所以其时间复杂度为O(n)。
总结
归并排序和快速排序是两种稍微复杂的排序算法,它们用的都是分治的思想,代码都通过递归来实现,过程非常相似。理解归并排序的重点是理解递推公式和 merge()合并函数。同理,理解快排的重点也是理解递推公式,还有 partition() 分区函数。归并排序算法是一种在任何情况下时间复杂度都比较稳定的排序算法,这也使它存在致命的缺点,即归并排序不是原地排序算法,空间复杂度比较高,是 O(n)。正因为此,它也没有快排应用广泛。
快速排序算法虽然最坏情况下的时间复杂度是 O(n ),但是平均情况下时间复杂度都是O(nlogn)。不仅如此,快速排序算法时间复杂度退化到 O(n)的概率非常小,我们可以通过合理地选择 pivot 来避免这种情况。
课后思考
现在你有 10 个接口访问日志文件,每个日志文件大小约 300MB,每个文件里的日志都是按照时间戳从小到大排序的。你希望将这 10 个较小的日志文件,合并为 1 个日志文件,合并之后的日志仍然按照时间戳从小到大排列。如果处理上述排序任务的机器内存只有1GB,你有什么好的解决思路,能“快速”地将这 10 个日志文件合并吗?
@峰
每次从各个文件中取一条数据,在内存中根据数据时间戳构建一个最小堆,然后每次把最小值给写入新文件,同时将最小值来自的那个文件再出来一个数据,加入到最小堆中。这个空间复杂度为常数,但没能很好利用1g内存,而且磁盘单个读取比较慢,所以考虑每次读取一批数据,没了再从磁盘中取,时间复杂度还是一样O(n)。
有问题?发送 issues 给我~