13-线性排序：如何根据年龄给100万用户数据排序？

Posted on | Post modified:
Words count in article: 2.5k | Reading time ≈ 9

这一讲我们来分析三种时间复杂度是O(n)的排序算法：桶排序、计数排序、基数排序。由于他们算法的时间复杂度是线性的，所以我们把这类排序算法又叫做 线性排序。之所以能做到线性的时间复杂度，主要原因是，这三个算法是 非基于比较的排序算法，都不涉及元素之间的比较操作。这几种排序算法理解起来、分析时间、空间复杂度都不难，但是对数据的要求很苛刻，所以 重点掌握这些算法的适用场景。

按照惯例，我们来看一道思考题：如何根据年龄给100万用户排序而时间复杂度是O(n)呢？

桶排序(Bucket sort)

它的核心思想是将要排序的数据分到几个有序的桶里，每个桶里的数据再单独排序。桶内排完序后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。

很简单的思路，我们来看看这张图：

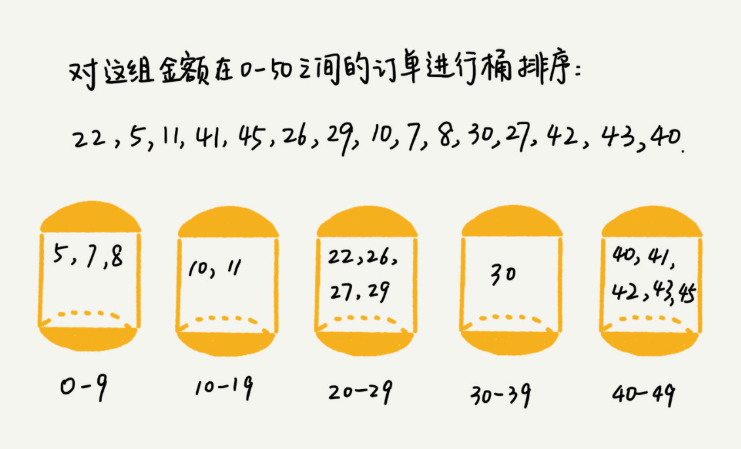
bucketSort

你可能会很奇怪，这样的排序方法时间复杂度怎么会是O(n)呢？下面我们就来分析一下：

如果要排序的数据有n个，我们把它们均匀的划分到m个桶中，每个桶中就有k = n / m个数据。我们让每个桶内都使用快速排序，那么它们的时间复杂度是O(m k logk), 再套用上面式子将k替换掉时间复杂度就是O(nlogn/m),当桶的个数m接近总的数据个数，那么logn/m将是一个很小的量，于是它的时间复杂度就是O(n)了。(结合上面的图读你可能就意识到这要求是有多变态了。。are you kidding me??)

我们可以看到：

  1. 要排序的数据需要很容易就能划分成m个桶，并且，桶与桶之间有着天然的大小顺序。
  2. 数据在每个桶之间分布是比较均匀的。如果数据通过桶的划分之后，有些桶的数据非常多，有些非常少，那桶内数据排序的时间复杂度就不是常量级了。在极端的情况下，如果数据都被划分到一个桶里，时间复杂度就会退化成O(nlogn)了。

桶排序的场景

既然桶排序要求这么苛刻，那么它到底适用于什么场景呢？桶比较适合用在外部排序中。外部排序就是，当数据存储在外部磁盘中，数据比较大，而内存有限无法一次性将它们全部加载到内存中的情况下进行排序。

计数排序(Counting sort)

计数排序就是桶排序的一种特殊情况。当要排序的n个数据，所处的范围并不大的时候，比如最大值是k，这样就可以把数据划分成k个桶，每个桶内的数据值都是相同的，省掉了桶内的排序时间。

这个算法很巧妙，我们来看看算法的核心思想(这个过程最好在纸上画画)。我们用一个具体的例子来描述。现有一个乱序数组A，里面有8个元素2，5，3，0，2，3，0，3(数字对应的是分数，比如第一个就是2分)。现在要把它排序好放入数组R中。我们观察到这八个元素它们取值区间为0~5，现在来创建一个数组C[6]。场景是这样的，第一步，数组的下标是分数，元素值为对应分数的学生个数；第二步，我们再将里面的元素值变为当前值与前面一个元素值的和。所以现在数组C的变化是这样的：

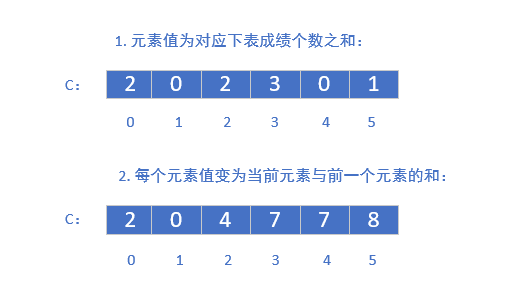
countingSortArray

好了，现在我们来整理一下，这会儿呢我们有三个数组，A、R、C。现在倒序遍历A。第一个元素a[n-1]为3，那么我们就去找c[3],它的值为7，也就是说，小于等于分数3的个数有7个，对应了r中第七个元素的位置(下标为6)，并且这是有序数组中最后一个3。这时，让c[3]中的值减一变为6(当下次遍历到3时就直接可以放入到r[5]的位置)。

下面我们来看看代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
// 计数排序，a是数组，n是数组大小，假设数组中存储的都是非负整数。

public void countingSort(int[] a, int n) {
  if(n <= 1) {
    return;
  }
  
  // 查找数组中数据的范围
  int max = a[0];
  for(int i = 1; i < n; ++i) {
    if(max < a[i]) {
      max = a[i];
    }
  }
  
  // 申请一个计数数组c，下标大小为[0, max], 初始化c
  int[] c = new int[max + 1];
  for(int i = 0; i <= max; ++i) {
    c[i] = 0;
  }
  
  // 将当前值与前一个值求和最后又赋值还给当前值
  for(int i = 1; i <= max; ++i) {
    c[i] = c[i-1] + c[i];
  }
  
  // 申请临时数组r，存储排序之后的结果
  int[] r = new int[n];
  for(int i = n; i >= 0; --i) {
    int index = c[a[i]] - 1;  // 取出c中下标为a[i]的值，另其-1赋值给数组r的下标
    r[index] = a[i];  // 找到a[i]在r中的位置，放入r中
    c[a[i]]--;  // 将c中下标为a[i]的值-1
  }
  
  // 将结果拷贝给还数组a
  for(int i = 0; i < n; ++i) {
    a[i] = r[i];
  }
}

计数排序只能用数据范围不大的场景，如果数据范围k比要排序的数组n大很多这个排序就不适用了。而且，计数排序只能给非负整数排序，如果要排序的数组是其它类型的，就要将其在不改变大小的情况下转换为非负整数。

基数排序(Radix sort)

我们再来看一个排序问题：假设我们有10万个手机号码，希望将这十万个手机号码从小到大排序，有什么比较快速的算法呢？

我们之前有讲到快排，时间复杂度可以做到O(nlogn)，那么还有更高效的方法嘛？桶排序和计数排序显然不行，手机号码有11位，范围太大。针对这个问题，我们来介绍一下基数排序。

它的算法思想是，倒着来排，即从最后一位开始排序，接着倒数第二位，以此类推，经过十一次排序，手机号码就有序了。

手机号码太长，这里用下面这张图片解说一下，原理是一样的：

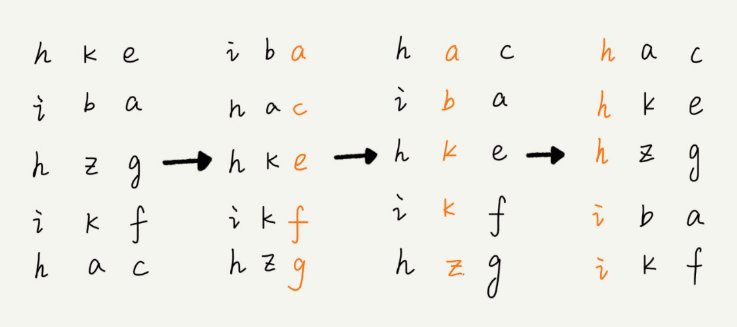
radixSort

需要注意的是，这里按照每位来排序的排序算法需要是稳定的。

实际上，有时候需要排序的数据并不都是等长的，比如需要排序英文字典里的单词，那这个时候我们应该怎么能解决这个问题呢？我们可以把所有的单词补齐到相同长度，位数不够的可以在后面补“0”。因为根据ASCII值，所有的字母都大于0，所以不会影响到它的排序。

基数排序对要排序的数据要求是可以分割出独立“位”的，而且位之间要有递进关系。如果a数据的高位比b数据大，那剩下的低位就不用比较了。除此之外，每一位的数据范围不能太大，要可以用线性排序算法来排序，否则基数排序的时间复杂度就无法做到O(n)了。

解答开篇

学了这三个排序，开篇提到的问题就显得很简单啦。年龄的范围在[1, 120]区间内，这样我们就可以根据桶排序，遍历这100万数据，根据年龄将它们划分到这120个桶里面，然后依次遍历这120个桶，得到的用户年龄就是有序的了。

内容小结

桶排序、计数排序和基数排序对数据的要求都比较严苛，所以应用不是特别广泛。但是如果数据的特征很符合算法的要求，那我们使用这些算法就会很高效，时间复杂度可以降到O(n)。

桶排序和计数排序非常相似，都是针对范围不大的数据，将数据划分成不同的桶来实现排序。基数排序要求数据可以划分成独立的位，位与位之间有递进关系。而且每一位的数据范围不能太大，否则就无法利用桶排序或者计数排序完成进而导致算法复杂度退化。

课后思考

假设我们现在需要对D、a、F、B、c、A、z 这个字符串进行排序，要求将其中所有小写字母都排在大写字母的前面，但小写字母内部不要求有序。这个应该如何实现呢？如果字符串中还有数字，仍然还是要求将小写字母放在前面，大写字母放在后面，不用排序算法又该怎么解决呢？

@wujc
用两个指针a、b：a指针从头开始往后遍历，遇到大写字母就停下，b从后往前遍历，遇到小写字母就停下，交换a、b指针对应的元素；重复如上过程，直到a、b指针相交。
对于小写字母放前面，数字放中间，大写字母放后面，可以先将数据分为小写字母和非小写字母两大类，进行如上交换后再在非小写字母区间内分为数字和大写字母做同样处理

@伟忠
课后思考，利用桶排序思想，弄小写，大写，数字三个桶，遍历一遍，都放进去，然后再从桶中取出来就行了。相当于遍历了两遍，复杂度O(n)

有问题？发送 issues 给我~

0%