前面讲的都是线性表结构、栈、队列等待。我们今天就来讲讲一种非线性结构,树。我们会分四节来学习。(有没有好激动?我好激动呀 ( ̄▽ ̄)” ~ )
废话不多说,这一讲我们主要介绍一下树。不过,在开始之前,我们再来看看题头的问题,什么样的二叉树适合用数组来存储呢?也许你已经有答案了,现在就开始啦。
树(Tree)
什么是树?来看看维基百科的解释:
树(tree)是一种抽象数据类型(ADT)或是实作这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
看看下面这张图,你也许会更加清楚的明白: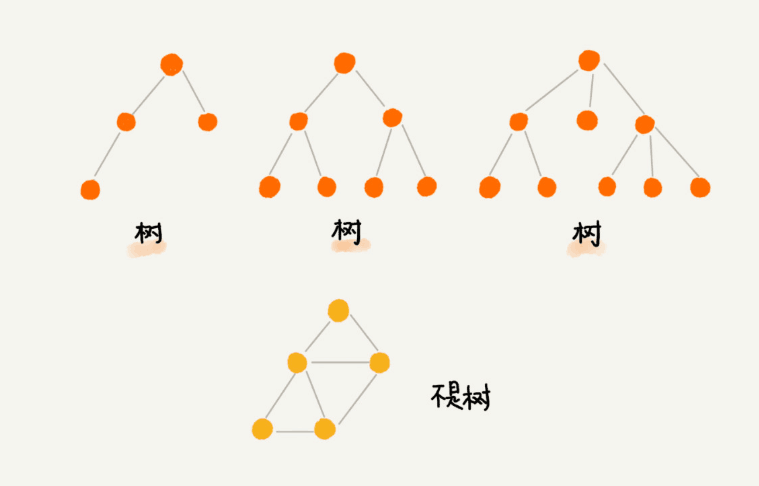
再比如下面这幅图,A节点就是B节点的 父节点,B节点是A节点的 子节点。B、C、D这三节点的父节点是同一个,因此,我们称它们为 兄弟节点。我们把没有父节点的节点称为 根节点。把没有子节点叫做 叶子节点。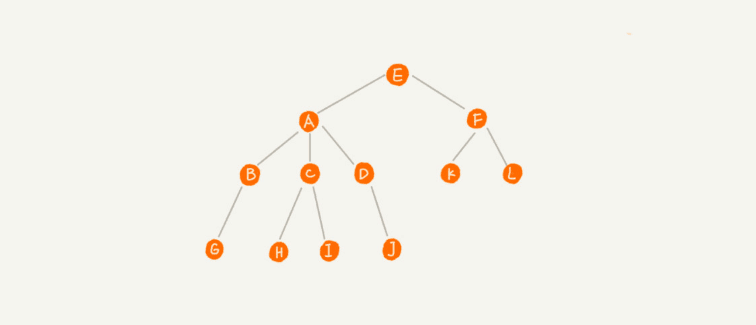
除此之外,还有三个需要清楚的概念:高度、深度、层。它们的定义是这样的:
这三个概念容易混淆,我们用个例子来看看: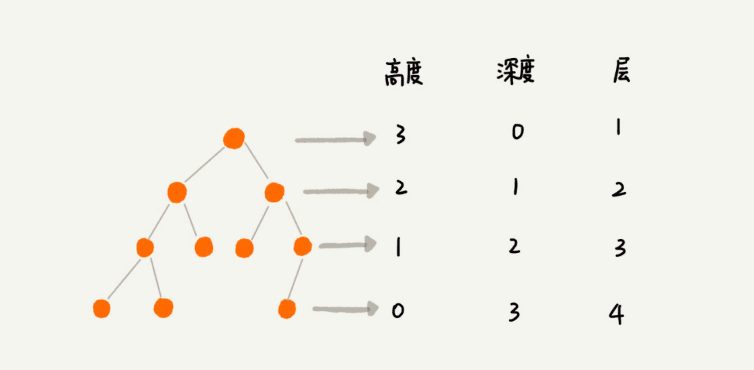
二叉树(Binary Tree)
树的结构多种多样,这里我们讲最常用的二叉树。二叉树,每个节点最多只有两个子节点,分别是 左子节点和 右子节点。
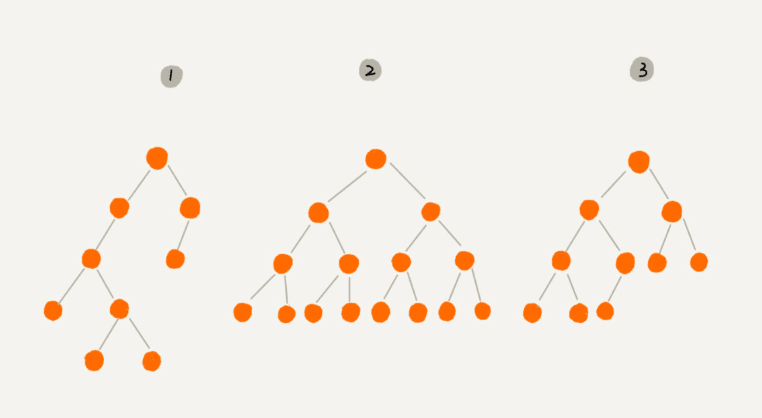
我们把,叶子节点全都在最底层,并且除了叶子节点外,其它每个节点都有左右两个子节点,这种二叉树叫做 满二叉树(编号为2)。我们把,叶子节点都在最底下两层,最后一层的叶子节点都靠左,其它每个节点个数都达到最大,这种二叉树叫做 完全二叉树(编号为3)。
你可能会疑惑,为什么完全二叉树要求最后一层的叶子节点靠左排列呢?(当初学的时候,我想的是,因为靠左比较好看~~)
要理解完全二叉树定义的由来,我们需要先了解,如何存储一棵二叉树?
想要存储一棵二叉树,我们有两种方法,一种是基于指针或者引用的 二叉链式存储法,一种是基于数组的 顺序存储法。
第一种链式存储法比较直观,每个节点有三个字段,其中一个存数据,另外两个分别指向左右两个子节点。我们只需要知道根节点,整棵树就都能找着了。
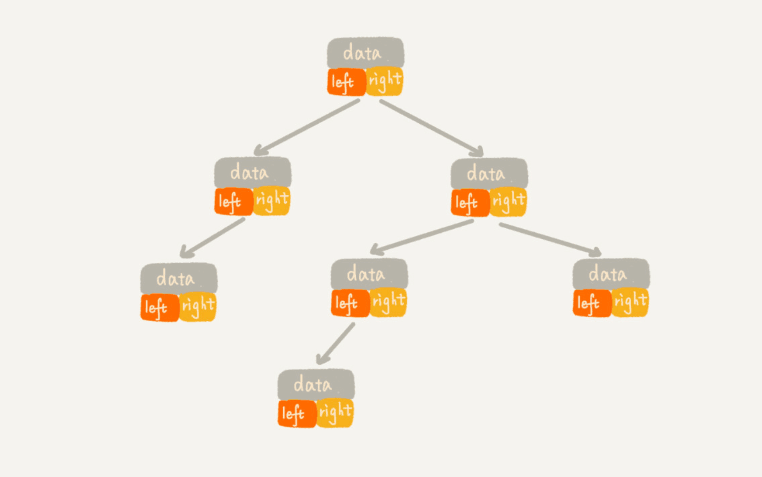
第二种就是顺序存储法了。我们把根节点存储在下标i = 1的位置,它的左节点存储在下标2 i = 2的位置,右节点存储在 2 i + 1 = 3的位置。以此类推, 设节点X的下标为i,那它的左节点下标为 2 i(如果有的话),右节点下标为 2 i + 1(如果有的话),它的父节点就是 i / 2 (通常,为了方便计算子节点,根节点会存储在下标为1的位置)。
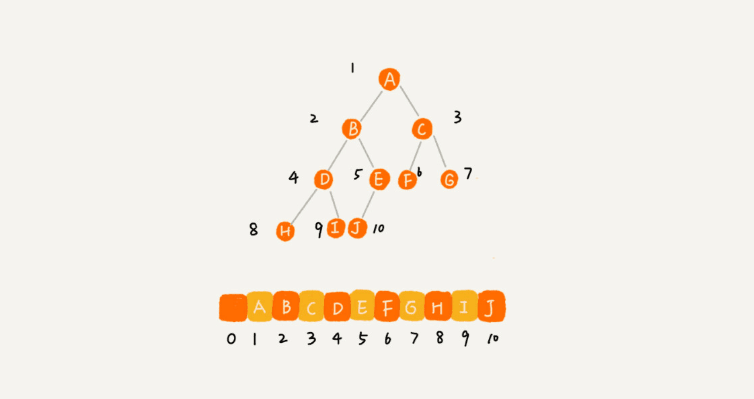
看,在这个数组里面,除了下标为0的元素,其它所有的数据都是连续存储的。但是如果是非完全二叉树(可能没有左节点),那中间就可能有空位置。这也就是为什么完全二叉树的最后一层的子节点都靠左的原因了。
二叉树的遍历
前面我们讲了二叉树的基本定义和存储方法。现在我们来看看二叉树中非常重要的操作,二叉树的遍历。
如何将所有节点都遍历打印出来呢?经典的方法有三种,前序遍历、中序遍历、和 后序遍历。其中,前、中、后表示的是节点与它的左右子树节点遍历打印的先后顺序。
- 前序遍历,对树中的任意节点来说,先打印节点本身,然后打印它的左子树,最后打印它的右子树。
- 中序遍历,对树中的任意节点来说,先打印它的左子树,然后再打印它的本身,最后打印它的右子树。
- 后序遍历,对于树中的任意节点来说,先打印左子树,然后打印右子树,最后才打印节点本身。
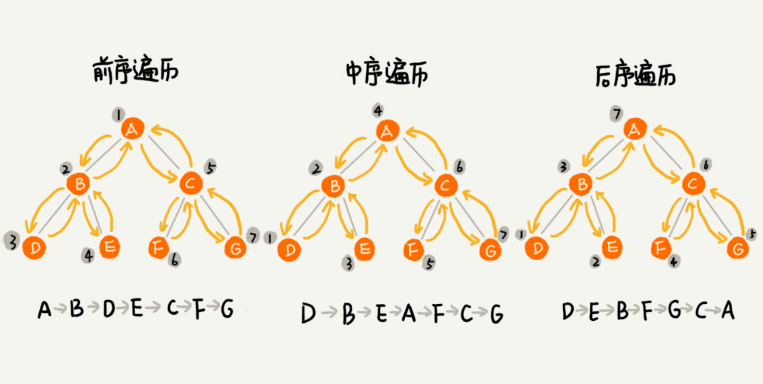
实际上,二叉树的前、中、后序遍历就是一个递归的过程。 之前我们在递归那篇文章中提过,写递归主要是要推出递推公式。
1 | // 前序遍历 |
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28void preTraversal(Node* root) {
if(root == null) {
return ;
}
printf("%d ", root->data);
preTraversal(root->left);
preTraversal(root->right);
}
// 中序遍历
void inTraversal(Node* root) {
if(root == NULL) {
return ;
}
inTraversal(root->left);
printf("%d ", root->data);
inTraversal(root->right);
}
// 后序遍历
void postTraversal(Node* root) {
if(root == NULL) {
return ;
}
postTraversal(root->left);
postTraversal(root->right);
printf("%d ", root->data);
}
这样看就很简单啦。现在我们要看看它们的时间复杂度。从上面的代码,我们可以看出来,每个节点最多会被访问两次,所以遍历操作的时间复杂度与节点的个数n成正比,也就是,时间复杂度为O(n)。
解答开篇 & 内容小结
这一篇,我们讲了一种非线性表数据结构,树。关于树有几个常用的概念,根节点、叶子节点、父节点、子节点、兄弟节点和树的高度、深度、层。
我们常用的树就是二叉树。二叉树的每个节点最多有两个子节点。二叉树中也有两种比较特殊的树,分别是满二叉树和完全二叉树。前后又是后者的一种特殊情况。
二叉树既可以用链式存储,也可以用数组顺序存储。数组顺序存储的方式比较适合完全二叉树,其它类型的二叉树用数组存储会比较浪费内存空间。除此之外,二叉树里非常重要的操作就是前、中、后序遍历操作,它们的时间复杂度都是O(n)。
课后思考
- 给定一组数据,比如 1,3,5,6,9,10。算算它们可以构建出多少不同的二叉树?
- 我们讲了三种二叉树的遍历。实际上,还有另外一种遍历方式,就是按层遍历,你知道如何实现嘛?
@失火的夏天
1、是卡特兰数,是C[n,2n] / (n+1)种形状,c是组合数,节点的不同又是一个全排列,一共就是n!*C[n,2n] / (n+1)个二叉树。可以通过数学归纳法推导得出。
2、层次遍历需要借助队列这样一个辅助数据结构。(其实也可以不用,这样就要自己手动去处理节点的关系,代码不太好理解,好处就是空间复杂度是o(1)。不过用队列比较好理解,缺点就是空间复杂度是o(n))。根节点先入队列,然后队列不空,取出对头元素,如果左孩子存在就入列队,否则什么也不做,右孩子同理。直到队列为空,则表示树层次遍历结束。树的层次遍历,其实也是一个广度优先的遍历算法。
@言志
1、既然是数组了,说明是完全二叉树,应该有n的阶乘个组合。
2、二叉树按层遍历,可以看作以根节点为起点,图的广度优先遍历的问题。
有问题?发送 issues 给我~